Istorijski kontekst
Početkom XX veka fizičari su znali da atom sadrži elektrone i malo, pozitivno naelektrisano jezgro (Radefordov eksperiment). Međutim, klasična elektrodinamika je tvrdila da elektron, kao naelektrisana čestica, ne može stabilno da kruži oko jezgra – gubio bi energiju i pao na jezgro. Planetarni model atoma je zato bio odbačen.
Dodatni problem predstavljali su linijski spektri: pobuđeni atomi ne emituju kontinualni spektar, već diskretne linije određenih talasnih dužina. Švedski fizičar Johanes Ridberg je empirijski pronašao formulu:
$ \frac{1}{\lambda} = R \left( \frac{1}{m^2} – \frac{1}{n^2} \right) $
gde je $R$ Ridbergova konstanta, a $m$ i $n$ celi brojevi. Uzrok ovih linija, međutim, nije bio poznat.
Borov model (1913)
Nils Bor je predložio model atoma zasnovan na tri postulata:
Prvi postulat
Elektron se kreće oko jezgra po stacionarnim kružnim orbitama, bez gubitka energije.
Drugi postulat
Na tim orbitama, moment impulsa elektrona je kvantizovan:
$ m v r = n \hbar $
gde je:
- $m$ – masa elektrona,
- $v$ – brzina elektrona,
- $r$ – poluprečnik orbite,
- $n$ – ceo broj (kvantni broj),
- $\hbar = \frac{h}{2\pi}$ – redukovana Plankova konstanta.
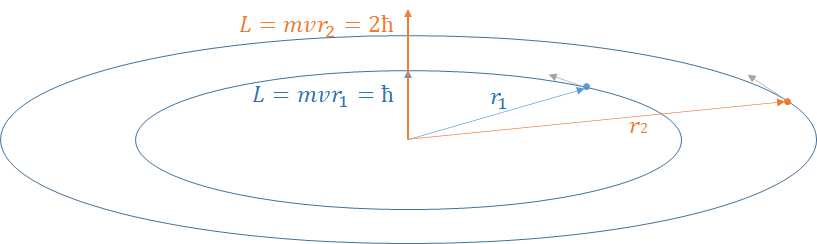
Iz ovog izraza dobijamo poluprečnik orbite:
$ r_n = \frac{n \hbar}{m v} $
Za prvu orbitu ($n=1$):
$ r_1 = \frac{\hbar}{m v} $
Za drugu orbitu ($n=2$):
$ r_2 = \frac{2 \hbar}{m v} $
i tako dalje.
Treći postulat
Elektron može da preskoči sa jedne orbite na drugu, pri čemu emituje ili apsorbuje energiju:
$ h \nu = E_{n_2} – E_{n_1} $
Ako elektron prelazi na niži nivo, emituje foton; ako prelazi na viši, apsorbuje foton.

Objašnjenje linijskih spektara

Pošto su energije orbita diskretne, razlike energija su takođe diskretne, pa su i talasne dužine emitovanih fotona strogo određene. Bor je dobio izraz za talasni broj:
$ \frac{1}{\lambda} = k \frac{hc}{1/n_1^2 – 1/n_2^2} $
što je u saglasnosti sa Ridbergovom formulom.

Značaj Borovog modela
- Objašnjava linijske spektre.
- Uvodi kvantizaciju u atomsku fiziku.
- Postavlja osnovu za razvoj kvantne mehanike.