$\alpha =45^0$

$d=0,80 m$

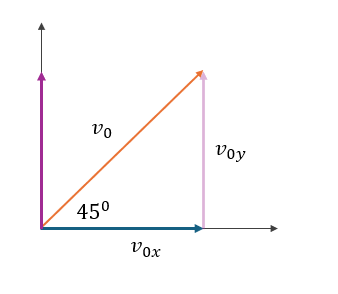
U pitanju je kosi hitac, što znači da ćemo kretanje skakavca razložiti na dva kretanja, koja se odvijaju simultano duž poznatih pravaca:

1. Po vertikalnom pravcu sa početnom brzinom $v_{0y}$ gde koristimo zakonitosti vertikalnog hica.
2. Po horizontalnom pravcu sa početnom brzinom $v_{0x}$ gde koristimo zakonitosti ravnomernog pravolinijskog kretanja.

Vertikalni hitac

Iz formule za trenutnu brzinu kod vertikalnog hica:

$v_{y}=v_{0y}-gt_{1}$

kada je visina maksimalna – $v_{y}=0$

pa sledi da je:

$v_{0y}=gt_{1}$

odakle se može izraziti vreme penjanja kao:

$t_{1}=\frac{v_{0y} }{g}$

Od odskoka do doskoka skakavca protekne dvostruko više vremena, jer penjanje i padanje traju isto, te je:

$t=2\cdot t_{1}=2\cdot \frac{v_{0y} }{g}$

Ravnomerno pravolinijsko kretanje

Gledano duž horizontalnog pravca, duž x ose, kretanje je ravnomerno pravolinijsko jer gravitacija koja deluje po vertikali ne utiče na brzinu duž x ose. Otuda se maksimalni domet skakavca od 0,80 m može iskazati kao:

$d=v_{0x}\cdot t$

Odnosno kada se zameni vreme iz prethodnog izraza:

$d=v_{0x}\cdot 2\frac{v_{0y} }{g}$

Pošto se skakavac svaki put odrazi pod uglom od $45^0$ vertikalna i horizontalna brzina su jednake jer pravougli trougao, koji komponente $v_{0x}$ i $v_{0y}$ grade sa brzinom $v_0$, ima jednake katete.

$v_{0x}=v_{0y}=v$

Tako da prethodni izraz možemo zapisati bez indeksa x i y kao:

$d=v\cdot 2\frac{v }{g}$

Kada pomnožimo $v$ i $v$

$d=2\frac{v^2}{g}$

odakle dobijamo da je srednja brzina kojom skakavac napreduje po horizontali:

$v^2=\frac{g\cdot d}{2}$

$v=\sqrt{\frac{g\cdot d}{2}}$

$v=1,98\frac{m}{s}$