Borov model atoma

Borov model atoma se temelji na tri postulata, koja predstavljaju atom kao sistem koji čine teško pozitivno jezgro i elektroni, raspoređeni po stabilnim energetskim nivoima. Pri tom je svaki prelazak elektrona između energetskih nivoa praćen emisijom ili apsorpcijom zračenja. Na ovaj način Bor je objasnio emisione spektre atoma.

Tri Borova postulata

Danski naučnik Niels Bohr je 1913. godine predložio novi model atoma. Ovaj model uvodi tri postulata (iskazi koji se ne dokazuju): 

1. Elektroni se oko jezgra kreću po stabilnim energetskim nivoima, pri čemu niti primaju niti gube energiju. 

2. Za orbite elektrona važi da je moment impulsa elektrona $ L=n\cdot \hbar $ gde je $ \hbar $ redukovana Plankova konstanta: ${h}/{2\pi }$.

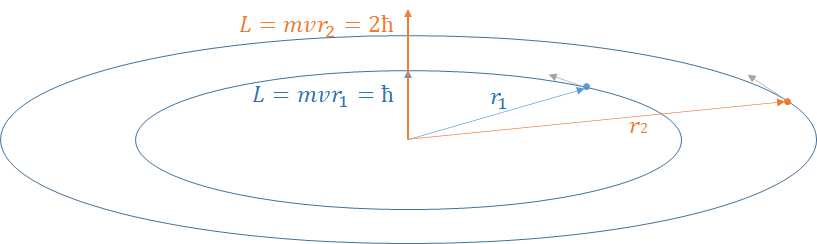
Tako da je, po Boru, moment impulsa elektrona na prvoj orbiti jednak $ \hbar $ , na drugoj orbiti 2$ \hbar $ i tako dalje. Bor nije objasnio kako je došao do ovih rezultata, ali je njegov treći postulat uspostavio teorijsku vezu sa prethodnim rezultatima proučavanja atomskih spektara, koji još nisu bili teorijski interpretirani.

3. Elektron može da skoči sa nižeg energetskog nivoa na viši energetski nivo samo ako pri tom apsorbuje energiju koja je jednaka energetskoj razlici krajnjeg i početnog nivoa. Pri skoku sa višeg na niži nivo, elektron emituje energiju u vidu fotona po istom principu.

Kada se oslobađa viška energije, elektron emituje foton odgovarajuće energije. Ukoliko mu se pruži prilika da takav foton apsorbuje, elektron dobijenu energiju iskoristi da skoči na viši energetski nivo. Svaki prelaz između energetskih nivoa praćen je apsorpciom fotona (na viši nivo) ili emisijom fotona (na niži nivo).

$$ h\nu =E_{m}-E_{n} $$

Prihvatajući Plankovu pretpostavku o kvantizaciji energije elektromagnetnih talasa, gde je $ E=h\nu $ i kombinujući to saznanje sa pretpostavljenim kvantizovanim vrednostima za moment impulsa elektrona $ L=n\cdot \hbar $ , Bor dolazi do talasnog broja zračenja koje se emituje ili apsorbuje pri elektronskom prelazu sa nivoa n₂ na nivo n₁:

$$\frac{1}{\lambda } =\frac{k}{hc}\cdot \left(\frac{1} {n^{2 }_ {1 } } – \frac{1} {n^{2 }_ {2 } } \right)$$

$ k $ u gornjoj formuli predstavlja konstantu izvedenu iz osnovnih konstanti, mase i naelektrisanja elektrona kao i Plankove konstante.

Iako je na ovaj način dao teorijsku interpretaciju emisionih spektara atoma, Bor i dalje nije uspeo da izmiri svoj model atoma sa zakonima elektrodinamike, koji zabranjuju elektronima da se kreću ubrzano, a kretanje po svakoj zakrivljenoj putanji jeste ubrzano kretanje.