Ketanje tela po kružnici opisuje se uglom zakretanja, kružnom brzinom i kružnim ubrzanjem.
Veličine kojima se opisuje kružno kretanje
Video čas
Iako se nama čini da su pravolinijsko i kružno kretanje potpuno različiti tipovi kretanja, s obzirom na putanju – nije tako. Setite se samo da svaki put kada hodate ulicom ili se vozite putem, vi u stvari idete po krivoj liniji, zato što je Zemlja okrugla. Ali ta zakrivljenost putanje za vas je neprimetna, jer je poluprečnik Zemlje mnogostruko veći od dužine puta koji možete da sagledate. Dakle, pravolinijsko kretanje je u stvari kretanje po kružnici beskonačno velikog poluprečnika. Ovo znači da zakoni fizike, koji regulišu pravolinijsko kretanje moraju važiti i za kružno kretanje. Međutim, to nas ne sprečava da odaberemo specifičan set veličina kojima ćemo kružno kretanje opisivati lakše.
Položaj tela na kružnici je najlakše predstaviti položajem poluprečnika, koji se proteže od centra kružnice do tačke u kojoj se nalazi telo.
Ovaj poluprečnik se naziva vektor položaja tela. Svaka promena položaja tela, dok se kreće po kružnici, se tada lakše predstavlja merenjem ugla za koji se zakrene vektor položaja, nego merenjem puta koji telo prelazi po kružnici. Put koji telo prelazi, dok se kreće po kružnici bi morao da se meri po krivoj liniji, odnosno luku kružnice, što baš i nije tako jednostavno. Lakše je meriti ugao za koji se zakrene vektor položaja, koji se upravo i naziva ugao zakretanja.
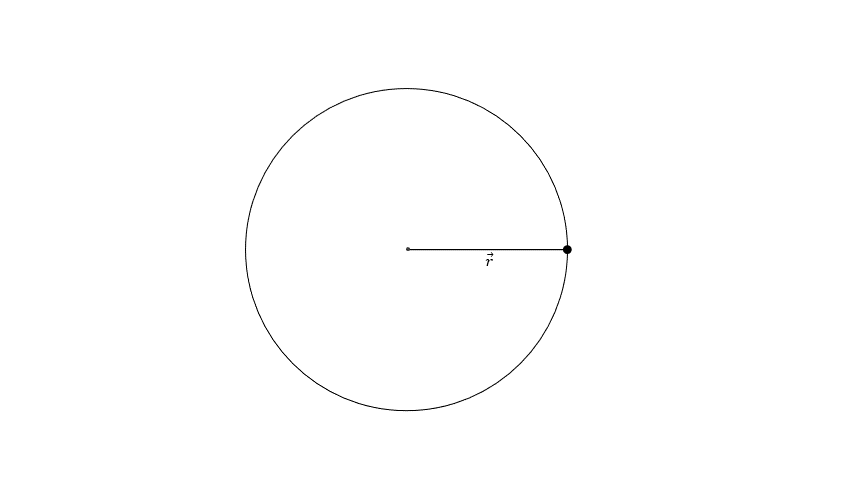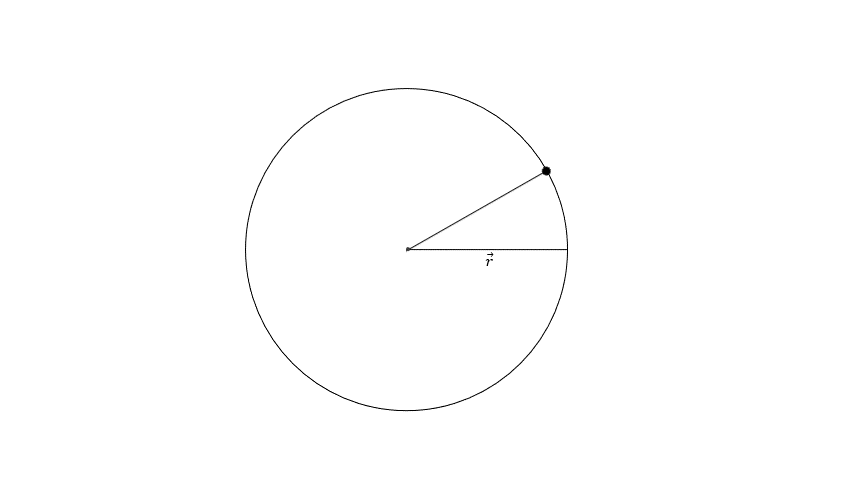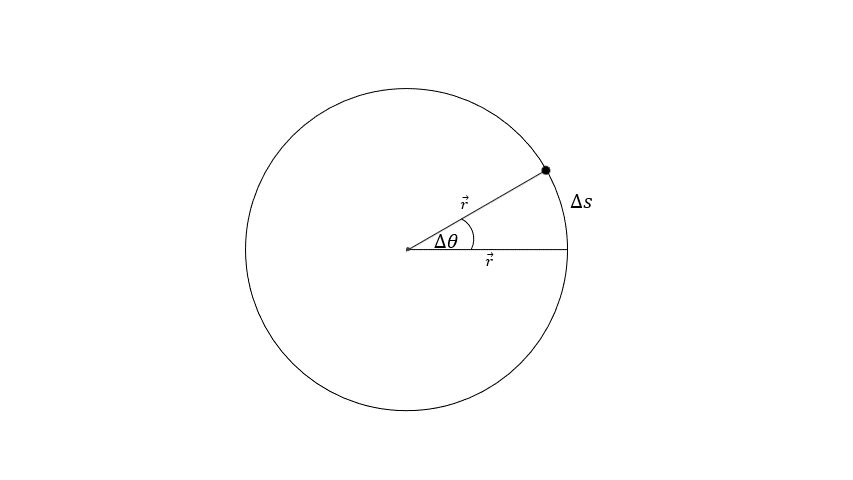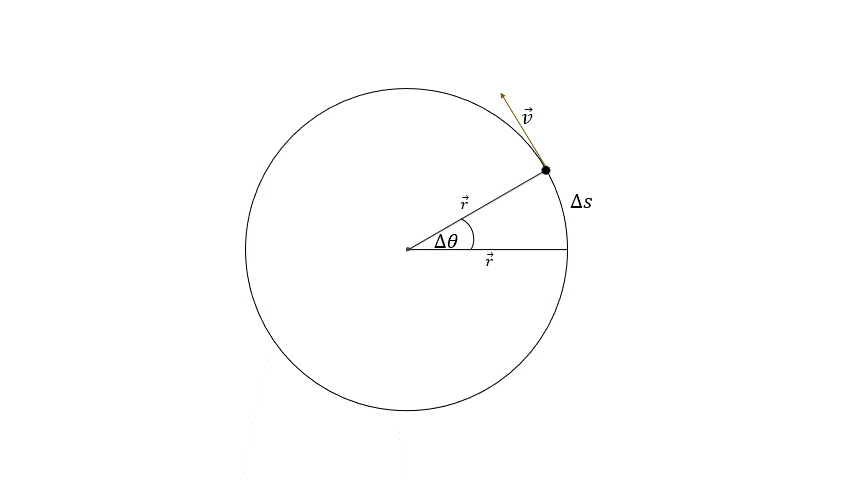
Kako bismo usaglasili kružno i pravolinijsko kretanje, moramo pronaći način da dužinu luka, koji telo pređe, izrazimo preko ugla zakretanja vektora položaja. Očigledno je da će telo koje se kreće po kružnici većeg poluprečnika, preći veću dužinu luka. Isto tako, ako se vektor položaja zakrene za veći ugao, dužina puta koji telo pređe će biti veća. Dakle, mogli bismo pređeni put $s$ da izrazimo kao proizvod poluprečnika $r$ i ugla zakretanja $\theta$, $$s=r\cdot \theta$$ Međutim, ako bismo zamenili brojne vrednosti u prethodni izraz, na osnovu postojećih mernih jedinica, dobili bismo pogrešan rezultat. Naime, ako se telo kreće po kružnici poluprečnika 1 m i pri tom se njegov vektor položaja zakrene za 360o, za dužinu puta bismo dobili vrednost od 360 m, što je očigledno pogrešan rezultat. Prema tome, treba nam neka nova jednica za merenje vrednosti ugla, koja bi nam za prethodnu situaciju dala rezultat $s=2\pi$ m, jer toliko iznosi obim kruga, čiji je poluprečnik $r=$ 1 m.
Nova jedinica za ugao, koja ispunjava prethodni uslovi da za pun krug ima vrednost od $2\pi$, se naziva radijan [rad]. Koristeći već definisanu vezu između dužine pređenog puta $s$, dužine vektora položaja $r$ i ugla zakretanja $\theta$, $s=r\cdot \theta$, te primenom radijana kao jedinice za ugao, dobijamo tačan rezultat da je pređeni put po obimu kružnice, poluprečnika $r=$ 1 m, $s=2\pi$ m. Ali, ne važi ova veza samo za dužinu puta po celoj kružnici, već za bilo koji kružni luk, odnosno za bilo koji ugao zakretanja, izražen u radijanima. Na ovaj način smo povezali pravolinijsku veličinu pređeni put $s$ sa kružnom veličinom ugao zakretanja $\theta$.
Pošto smo odabrali ugao zakretanja, kao osnovnu veličnu kojom opisujemo položaj tela na kružnici, kao i promenu tog položaja, treba definisati i veličinu koja će nam dati uvid u brzinu zakretanja vektora položaja, dok se telo kreće po kružnici. Ova veličina se naziva kružna brzina, označava se grčkim slovom ω a merna jedinica je rad/s.
$$\vec{\omega }=\frac{\Delta \theta }{\Delta t}$$
Kružna brzina iskazuje za koliki ugao se zakrene vektor položaja, svake sekunde.
Kružna brzina $\vec{\omega }$ je vektorska veličina. Pravac kružne brzine je pravac ose oko koje se telo kreće, a smer se određuje pravilom desne ruke. Kada prsti pokazuju smer obilaska tela po kružnici, palac pokazuje smer kružne brzine.
Ukoliko se kružna brzina menja tokom vremena, postoji i kružno ubrzanje, koje se obeležava grčkim slovom α a jedinica je rad/s2.
$$\vec{\alpha}=\frac{\Delta \vec{\omega}}{\Delta t}$$
Kružno ubrzanje $\vec{\alpha}$ ima isti pravac kao i kružna brzina $\vec{\omega}$, a smer zavisi od toga da li se kružna brzina tokom vremena povećava ili smanjuje. Kada se kružna brzina tokom vremena povećava $\vec{\alpha}$ i $\vec{\omega}$ imaju iste smerove, a ako se kružna brzina smanjuje, smerovi su im suprotni.
Sve kružne veličine su povezane sa svojim analognim pravolinijskim veličinama na isti način. Poveznica je poluprečnik kružnice, po kojoj se telo kreće. Što je veći poluprečnik kružnice, veće su i analogne pravolinijske veličine.
$$s=r\cdot \theta$$
$$v=r\cdot \omega$$
$$a=r\cdot \alpha$$