Uvod
Krajem XIX i početkom XX veka fizika je doživela revoluciju. Jedan od fenomena koji je izazvao veliku nedoumicu bio je fotoelektrični efekat – proces u kojem svetlost izbacuje elektrone iz metala.
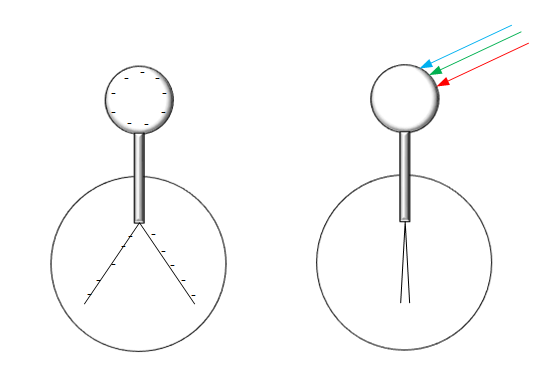
Eksperiment:
- Elektroskop se naelektriše (pozitivno ili negativno).
- Kada ga obasja ultraljubičasta svetlost, negativno naelektrisani elektroskop se razelektriše, dok pozitivno naelektrisani ostaje nepromenjen.
Zašto? Zato što UV svetlost izbacuje elektrone iz metala.
Problem klasične fizike
Prema Maksvelovoj teoriji, svetlost je elektromagnetni talas. Logično bi bilo da jačina efekta zavisi od intenziteta svetlosti i da svetlost veće talasne dužine (duže izlaganje električnom polju) izazove jači efekat.
Ali eksperimenti su pokazali:
- Svetlost velike talasne dužine → efekat izostaje.
- Svetlost male talasne dužine (UV) → efekat prisutan.
Klasična teorija nije mogla da objasni ovaj rezultat.
Ajnštajnovo objašnjenje (1905)
Albert Ajnštajn je predložio revolucionarnu ideju:
Svetlost ima talasno-čestičnu prirodu – može se posmatrati i kao talas i kao čestica (foton).
Foton nosi energiju:
$ E = h \nu $
gde je:
- $h = 6.62 \times 10^{-34}\text{J·s}$ – Plankova konstanta,
- $\nu$ – frekvencija svetlosti.
Mehanizam fotoelektričnog efekta
- Foton pogodi elektron u metalu i prenese mu energiju $E = h\nu$.
- Elektron mora savladati izlazni rad metala (oznaka $W$) da napusti površinu.
- Ako mu ostane energije, ona se pojavljuje kao kinetička energija elektrona:
$ h\nu = W + E_k $
gde je:
- $W$ – izlazni rad metala,
- $E_k$ – kinetička energija izbačenog elektrona.
Zašto efekat izostaje pri velikim talasnim dužinama?
Talasna dužina $\lambda$ i frekvencija $\nu$ su povezane:
$ \nu = \dfrac{c}{\lambda} $
Ako je $\lambda$ velika → $\nu$ mala → $E = h\nu$ mala.
Ako $E < W$, elektron ne može napustiti metal → efekat izostaje.
Prag frekvencije
Postoji granična frekvencija $\nu_0$ ispod koje efekat ne nastaje:
$ h\nu_0 = W $
Za talasne dužine veće od $\lambda_0 = \dfrac{c}{\nu_0}$ fotoelektrični efekat ne postoji.
Značaj otkrića
- Ajnštajn je za ovo objašnjenje dobio Nobelovu nagradu 1921. godine.
- Uvođenje talasno-čestičnog dualizma svetlosti otvorilo je put ka kvantnoj mehanici.