1. Šta je matematičko klatno?
Matematičko klatno je idealizovani model oscilatora koji se sastoji od:
- kuglice zanemarljivih dimenzija, mase $m$,
- neistegljivog konca dužine $l$, zanemarljive mase,
- čvrstog oslonca na koji je konac pričvršćen.
Kada kuglicu iz ravnotežnog položaja pomerimo i pustimo, ona počinje da osciluje levo-desno oko tog položaja. Ovo kretanje nazivamo oscilatorno kretanje.
2. Sile koje deluju na klatno
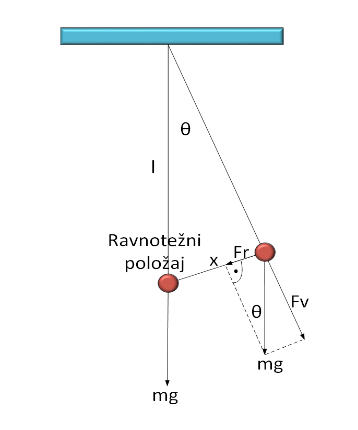
Na kuglicu deluje:
- sila gravitacije $mg$ (vertikalno nadole),
- sila zatezanja konca $F_z$ (duž konca),
- komponenta sile gravitacije koja vraća kuglicu u ravnotežni položaj – restituiciona sila $F_r$.
Ako konac zaklapa ugao $\theta$ sa vertikalom, komponenta sile koja vraća kuglicu u ravnotežni položaj je:
$ F_r = mg \sin \theta $
Za male uglove ($\theta < 10^\circ$), možemo koristiti aproksimaciju:
$ \sin \theta \approx \theta \quad (\text{u radijanima}) $
pa je:
$ F_r \approx mg , \theta $
3. Veza između ugla i elongacije
Za male oscilacije, put koji kuglica pređe od ravnotežnog položaja do amplitudnog položaja približno je jednak elongaciji $x$. Kod kružnog kretanja važi:
$ s = l \cdot \theta $
Dakle:
$ x \approx l \cdot \theta \quad \Rightarrow \quad \theta = \frac{x}{l} $
Vraćamo u izraz za restitucionu silu:
$ F_r = – mg \cdot \frac{x}{l} $
Minus označava da je sila uvek usmerena ka ravnotežnom položaju (suprotno od elongacije).
4. Poređenje sa harmonijskim oscilatorom
Opšti oblik restitucione sile kod harmonijskog oscilatora je:
$ F_r = -k x $
Iz poređenja dobijamo:
$ k = \frac{mg}{l} $
5. Period oscilovanja
Za harmonijski oscilator period je:
$ T = 2 \pi \sqrt{\frac{m}{k}} $
Zamenjujemo $k$:
$ T = 2 \pi \sqrt{\frac{m}{\frac{mg}{l}}} = 2 \pi \sqrt{\frac{l}{g}} $
Važna osobina:
Period oscilovanja ne zavisi od mase kuglice, već samo od dužine klatna $l$ i gravitacione konstante $g$.
6. Primena
Pošto možemo lako izmeriti dužinu klatna i period oscilovanja, matematičko klatno se koristi za eksperimentalno određivanje gravitacione konstante $g$.
Ključne formule:
- Restituiciona sila:
$ F_r = – mg \cdot \frac{x}{l} $ - Period oscilovanja:
$ T = 2 \pi \sqrt{\frac{l}{g}} $
